1. HOME > 約数、倍数、分数、素因数分解の計算の実例 >ルート3分の2を有理化した値は？1分でわかる求め方、小数、ルート4分の3、ルート3分の3の有理化は？

ルート3分の2を有理化した値は？1分でわかる求め方、小数、ルート4分の3、ルート3分の3の有理化は？

ルート3分の2を有理化した値は√6/3です。有理化とは分母に根号を含む式を、根号を含まない形に変形することです。√の値は二乗すると√が外れます。よって、√(2/3)を有理化する場合、分母と分子に√3を掛け算します。√(2/3)＝√(2/3)×√3/√3=√6/3になります。今回は、ルート3分の2を有理化した値、求め方、小数、ルート4分の3、ルート3分の3の有理化について説明します。有理化の意味は下記が参考になります。

有理化とは？1分でわかる意味、平方根、約分、分子との関係

ルート2分の1とは？1分でわかる計算、小数、２乗、有理化、角度、ルート2分の1分の1は？

管理人おすすめ書籍⇒　見るだけで理解が加速する　得点アップ　数学公式図鑑 [ あきとんとん ]

ルート3分の2を有理化した値は？求め方

ルート3分の2を有理化した値は√6/3です。有理化とは分母に根号（√）を含む式を、根号を含まない形に変形することです。√の値は二乗すると√が外れます。たとえば、(√a)^2=aです。よって、√(2/3)を有理化する場合、分母と分子に√3を掛け算すると

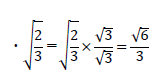
になります。有理化の求め方は下記が参考になります。

有理化とは？1分でわかる意味、平方根、約分、分子との関係

ルート3分の2の小数は？

ルート3分の2を小数に直すと約0.82です。前述したように、√(2/3)= √6/3です。√6≒2.45なので、√6/3＝√6÷3＝2.45÷3≒0.82になります。分数と小数の関係は下記をご覧ください。

分数とは？1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方

百分率と分数の関係は？1分でわかる変換、小数との関係、換算表、例題の計算

ルート4分の3、ルート3分の3の有理化は？

ルート4分の3、ルート3分の3を有理化した値を下記に示します。

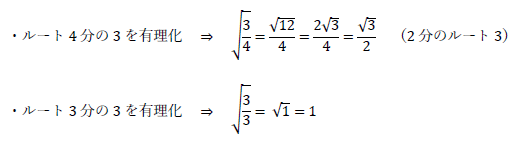
まとめ

今回は、ルート3分の2の値について説明しました。ルート3分の2を有理化すると√6/3になります。有理化とは分母に根号を含む式を、根号を含まない形に変形することです。有理化の計算、分数と小数の関係は下記が参考になります。

有理化とは？1分でわかる意味、平方根、約分、分子との関係

百分率と分数の関係は？1分でわかる変換、小数との関係、換算表、例題の計算

管理人おすすめ書籍⇒　算数と国語を同時に伸ばすパズル 入門編 [ 宮本 哲也 ]

プロフィール

• 略歴▼
• 名前　ハナダユキヒロ/換算と計算の実例 代表
• 2024年　弊サイトを開設


• これまで筆者は構造設計の実務に携わる中で様々な数量の単位換算を行ってきました。単位換算は「慣れ」です。


• 何度も繰り返し単位換算することで暗算できるようになります。弊サイトでは様々な単位換算の事例を解説し、学生、社会人の方に役立つ知識を、分かりやすくお伝えします。

同じカテゴリの記事一覧

• 分数の平方根の計算は？3分でわかる求め方、有理化、ルートの外し方は？
• 整数×ルートのやり方は？1分でわかる計算方法、ルートを含む整数との掛算の問題
• 整数÷ルートのやり方は？1分でわかる計算（割り算）、ルートの掛け算、足し算
• ルート2×ルート2は？1分でわかる答えと計算、ルート2の意味、2ルート2の二乗の答えは？
• ルート2÷ルート2は？1分でわかる答え、計算、ルート2×ルート2、2ルート2の二乗は？
• 2ルート2×2ルート2は？1分でわかる答え、求め方、2√2の答え、2√2÷2√2は？
• 2ルート2の答えは？1分でわかる計算、8との関係、例題の解き方
• 4ルート2の値は？1分でわかる計算、4ルート2掛ける2、4ルート2の半分、√と整数の掛け算は？
• ルート2分の1とは？1分でわかる計算、小数、２乗、有理化、角度、ルート2分の1分の1は？
• ルート2分の2の簡単な値は？1分でわかる求め方、2分のルート2の角度、sin45度はなぜ2分のルート2？