1. HOME > 三角関数 >cos135度の値は？1分でわかる求め方、分数の値、Sin135、sin120度、cos120度、sin150度、cos150度の値は？

cos135度の値は？1分でわかる求め方、分数の値、Sin135、sin120度、cos120度、sin150度、cos150度の値は？

cos135度の値は－1/√2（≒－0.707）です。単位円にθ＝135度の位置で半径を描きます。円と半径の交点からx軸に向かって垂線を引くと、鋭角が45度の直角三角形がつくれます。θ＝45度の直角三角形の辺の比率は「斜辺：底辺＝√2：1」です。また第二象限に位置するのでxは負の値になります。よって、cos135度＝底辺/斜辺＝－1/√2になります。今回は、cos135度の値と求め方、分数の値、Sin135、sin120度、cos120度、sin150度、cos150度の値について説明します。Sin135度、加法定理、２倍角の公式は下記をご覧ください。

sin135度の値は？求め方、三角比と2分のルート2、cos135度の値と求め方は？

三角関数の加法定理とは？3分でわかる意味、公式、応用と二倍角の公式

2倍角の公式とは？1分でわかる意味、求め方、問題、倍角の意味、証明

管理人おすすめ書籍⇒　見るだけで理解が加速する　得点アップ　数学公式図鑑 [ あきとんとん ]

cos135度の値は？分数の値、Sin135は？

cos135度の値は－1/√2（≒－0.707）です。下図をみてください。単位円にθ＝135度の位置で半径を描くと、鋭角が45度の直角三角形がつくれます。この直角三角形の辺の比率は「1：√2＝底辺（高さ）：斜辺」です。また、第二象限に位置するのでxは負の値になります。以上より、cos135度＝底辺/斜辺＝－1/√2ですね。

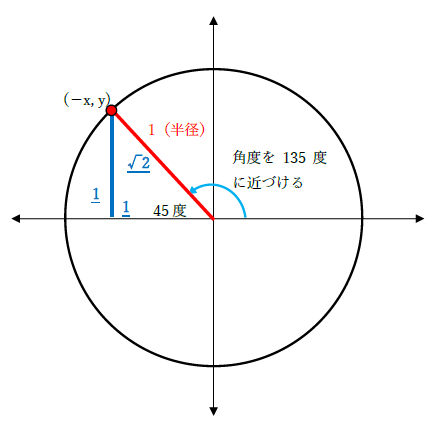
単位円の詳細は下記が参考になります。

単位円とは？1分でわかる意味、覚え方、表、sin、tanとの関係

また、加法定理を用いてcos135度の値を算定しても良いでしょう。加法定理を下記に示します。cos135度＝cos(45+90)度＝cos45cos90－sin45sin90を計算すれば良いですね。

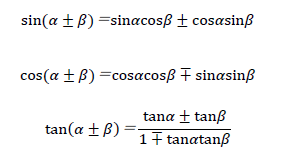
加法定理の詳細は下記が参考になります。

三角関数の加法定理とは？3分でわかる意味、公式、応用と二倍角の公式

また、sin135度は1/√2（≒0.707）です。高さは正の値なので、sin135度＝高さ/斜辺＝1/√2です。sin135度の詳細は下記をご覧ください。

sin135度の値は？求め方、三角比と2分のルート2、cos135度の値と求め方は？

sin120度、cos120度の値は？

sin120度、cos120度の値は下記の通りです。

・sin120度　⇒　√3/2（≒0.87）

・cos120度　⇒　－1/2

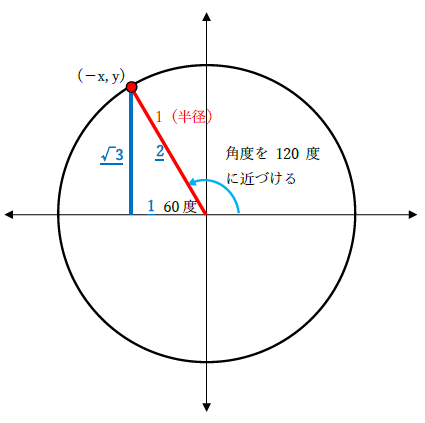
単位円にθ＝120度の位置で半径を描きます。半径と円の交点からx軸に向かって垂線をひくと、鋭角が60度の直角三角形がつくれます。このとき辺の比率は「√3：2：1＝高さ：斜辺：底辺」です。あとはsinθ＝高さ/斜辺、cosθ＝底辺/斜辺を計算すれば良いですね。sin120度、cos120度の詳細は下記をご覧ください。

sin120度の値は？1分でわかる求め方、分数、sin60度、cos120度、tan120度の値は？

cos120度の値は？【近日公開予定】

また、下記に示す2倍角の公式を使えばsin60度、cos60度を組み合わせた計算から、sin120度、cos120度が算定できます。

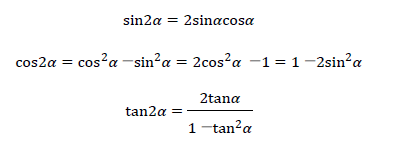
2倍角の公式は下記が参考になります。

2倍角の公式とは？1分でわかる意味、求め方、問題、倍角の意味、証明

sin150度、cos150度の値は？

sin150度、cos150度の値を下記に示します。

・sin150度　⇒　1/2（＝0.5）

・cos150度　⇒　－√3/2（≒－0.87）

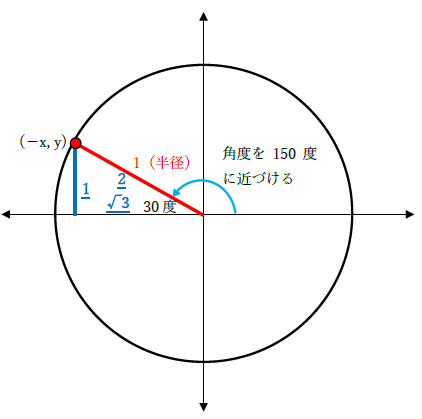
sin150度、cos150度の詳細は下記をご覧ください。

sin150度の値は？1分でわかる求め方、分数の値、sin15度、sin30度、sin120度の値は？

cos150度の値は？1分でわかる求め方、分数、sin150度、tan150度、Cos30度は？

まとめ

今回は、cos135度の値について説明しました。cos135度の値は－1/√2（≒－0.707）です。まずは単位円にθ＝135度の位置で半径を描きましょう。半径と円の交点からx軸に垂線を下すと、鋭角が45度の直角三角形がつくれます。辺の比率が1：√2なので、cos135度＝－1/√2ですね。加法定理、単位円、sin135度の求め方など下記も参考になります。

三角関数の加法定理とは？3分でわかる意味、公式、応用と二倍角の公式

単位円とは？1分でわかる意味、覚え方、表、sin、tanとの関係

sin135度の値は？求め方、三角比と2分のルート2、cos135度の値と求め方は？

管理人おすすめ書籍⇒　見るだけで理解が加速する　得点アップ　数学公式図鑑 [ あきとんとん ]

プロフィール

• 略歴▼
• 名前　ハナダユキヒロ/換算と計算の実例 代表
• 2024年　弊サイトを開設


• これまで筆者は構造設計の実務に携わる中で様々な数量の単位換算を行ってきました。単位換算は「慣れ」です。


• 何度も繰り返し単位換算することで暗算できるようになります。弊サイトでは様々な単位換算の事例を解説し、学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
• 広告・免責事項

同じカテゴリの記事一覧

• cos0度が1になる理由は？1分でわかる意味、覚え方、cos90度、cos180度の値は？
• cos30度の値は？1分でわかる分数、小数の値、求め方、cos45度、sin60度の値
• cos60度の分数は？1分でわかる値と求め方、cos30、cos45、sin60の分数は？
• cos75°の値は？1分でわかる求め方、加法定理との関係、分数の値、sin75°、tan75°の値は？
• cos90度の値は？1分でわかる求め方、0になる理由、sin90度、cos180度の値は？
• cos105度の値は？1分でわかる求め方、分数の値、加法定理との関係、cos105度+cos75度、cos105度+sin105度の値は？
• cos180度の値は？1分でわかる求め方、cos0度、cos90度、sin180度の値は？
• cos225度の値は？1分でわかる求め方、加法定理との関係、sin225度、tan225度の値
• cos240度の値は？1分でわかる求め方、分数の値、sin240度、tan240度、sin300度、cos300度の値は？
• cos270度の値は？1分でわかる求め方、sin270度、tan270度、cos90度、cos180度の値は？